نوبل فیزیک ۲۰۱۶ به پاس اثبات وجهی از عینیت ریاضیات

 در حالیکه گمانه‌زنی‌ها حاکی از آن بود که جایزه نوبل فیزیک امسال به داغ‌ترین خبر علمی سال هم مبنی بر کشف امواج گرانشی تعلق می‌گیرد (همانطور که در سال ۲۰۱۳ و در پی کشف ذره بوزون هیگز هم چنین شده بود)، اما جایزه امسال به دستاوردی از شاخه‌ای کاملاً متفاوت از فیزیک نظری تعلق یافت: فیزیک حالت جامد.

بنا بر تصمیم آکادمی سلطنتی علوم سوئد، نیمی از این جایزه به دیوید تولس از دانشگاه واشنگتن، و نیم دیگر آن نیز مشترکاً به دونکان هالدین از دانشگاه پرینستون و مایکل کاسترلیتز از دانشگاه براون، به پاس "کشفیات نظری‌شان مبنی بر وجود تغییر حالت‌های توپولوژیکی و حالت‌های توپولوژیکی ماده" تعلق یافت؛ مفاهیم نامأنوسی که کمترکسی حتی نام‌شان را در خارج از دنیای فیزیک شنیده است.

بخش اعظم جوایز نوبل فیزیک را می‌توان ذیل دو دسته تقسیم‌بندی کرد: از یک طرف جوایزی که به پاس برآوردن انتظارات دیرپای جامعه فیزیک اهدا شده‌اند، و از یک طرف نیز جوایزی که به ایده‌های درخشان منتهی به حل معماهای ژرف این رشته تعلّق گرفته‌اند. در حالی‌که نوبل‌های داغ فیزیک (همچون جوایز سالیان ۲۰۱۱ و ۲۰۱۳، به پاس کشف به ترتیب انرژی تاریک و ذره بوزون هیگز) معمولاً به دسته اول تعلق می‌گیرند، اما نوبل امسالِ فیزیک از دسته دوم بود.

با این وجود، اهمیت دستاوردهای منتهی به اعطای تک‌تک این جوایز را نمی‌توان دست‌کم گرفت؛ ولو برخی دستاوردها را نتوان به زبانی ساده بیان کرد. در این مقاله می‌کوشم تا اهمیت دستاوردی که نوبل فیزیک امسال به آن تعلق گرفت را در پرتو آن چشم‌اندازی که با کشف «حالت‌های توپولوژیک ماده» در برابر جامعه فیزیک و توسّعاً واقعیت فیزیکی گشوده شد، به بیان درآورم. 

پَرسه با پرتو ریاضیات

انتظارها برای اعطای نوبل فیزیک امسال به دست‌اندرکاران اصلی کشف امواج گرانشی بی‌دلیل نبود، و هنوز هم حدس اعطای نوبلی در آینده به آن بعید نمی‌نماید. وقتی جایزه نوبل فیزیک ۱۹۹۳ به جوزف تیلور و راسل هولس به پاس اثبات «غیرمستقیم» وجود امواج گرانشی تعلق یافت، قطعاً اثبات «مستقیم» این امواج هم سزاوار جایزه‌ای اگر نه نفیس‌تر، دست‌کم هم‌سنگ آن خواهد بود.

کشف امواج گرانشی که جسورانه‌ترین پیش‌بینی نظریه نسبیت عام اینشتین به شمار می‌آید، از این بابت اهمیت دارد که عریان‌ترین مدرک ممکن در دلالت بر «انحنای» فضا را عرضه می‌کند. هرچند که نسبیت عام اساساً نیروی گرانش را بر حسب همین انحناء  بازتعریف کرده است، اما اثبات صحّت این تعریف تاکنون فقط به میانجی یک «جرم» میسر بود؛ جرمی صرفنظر از ابعاد و جنس آن، که سابقاً در چارچوب روایت نیوتونی از گرانش، وجود آن تحت هر شرایطی برای برقراری این نیرو ضرورت داشت – به‌طوریکه در غیاب یک جرم، روایت نیوتونی نیز هیچ دلیلی برای استمرار وجود نیروی گرانش ِ ناشی از آن نمی‌دید. اما «امواج گرانشی»، به منزله انحناهایی مستقل از حضور جرم ِ مبدأشان در پیوستار فضا، دقیقاً آن برگ برنده‌ای بود که روایت نسبیتی از ماهیت گرانش را از نسخه نیوتونی آن متمایز می‌کرد؛ و کشف این امواج هم مدرکی دال بر آنکه روایت نیوتونی از گرانش، دیگر نسبتی با واقعیت ندارد.

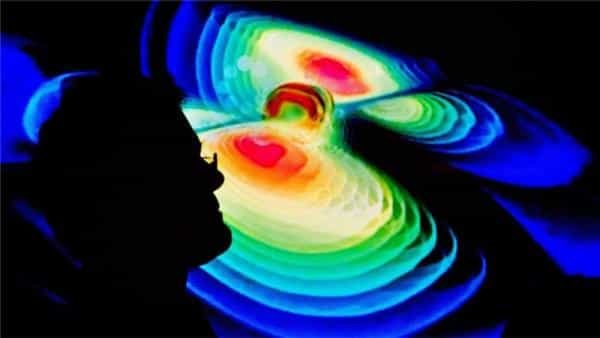
در پرتو اهمیت کشف امواج گرانشی، بهتر می‌توان به اهمیت دستاورد منتهی به نوبل فیزیک امسال هم پی برد: این جایزه نیز به اثبات مفاهیمی اختصاص یافته که در وهله اول از طریق حل معماهایی در ریاضیات محض صورت‌بندی شده بودند؛ بی‌کمترین تصوّری از امکان اطلاق‌شان بر پدیده‌های عینی ِ دنیای پیرامون. به عبارت دقیق‌تر، این مفاهیم انتزاعی – که در زهدانی جز عقل محض به عمل نیامده بودند – رفته‌رفته به منزله پرتوهایی عمل کردند که در فرآیندی به بلندای چندین قرن، رفته‌رفته از زوایایی یکسره ناملموس از جهان پرده برگرفتند؛ کشفیاتی نه در پرتو چشم، بلکه در پرتو عقل.

امکان‌‌پذیری تصوّر «انحنا»ی فضا، در وهله اول از طریق شاخه‌ای از ریاضیات محض موسوم به «هندسه نااقلیدسی» میسّر شده بود. در این نوع از هندسه، فقط یک اصل از اصول پنچ‌گانه هندسه اقلیدسی به رسمیت شناخته نمی‌شود؛ چراکه طبق ملاحظات دقیق، اصل پنجم اقلیدس نه گزاره‌ای منطقی، بلکه حکمی فلسفی و در واقع مبتنی بر یک پیش‌فرض تجربی است؛ پیش‌فرضی دال بر اینکه فضا تحت هر شرایطی «تخت» خواهد ماند (جهت مطالعه جزئیات استدلال منتهی به پیدایش هندسه نااقلیدسی، نگاه کنید به بخش «درنگ تاریخی: اقلیدس، خیام، و یک تلاش نافرجام»، از مقاله کشف امواج گرانشی: پژواک واقعیتی از جنس دیگر). اگرچه هنوز حتی یک قرن هم از کشف تجارب عینی و ابطال‌کننده این حکم نمی‌گذرد، اما صائب نبودن اصل پنجم اقلیدس، از حدود یک‌هزار سال پیش مشخص شده بود؛ یافته‌ای که دلالت‌های آن در تمام طول این مدّت فقط به یمن وجود زهدانی به استواری ریاضیات محض قادر شد که تا پشت مرزهای فیزیک پیشروی کند و به زیربنای نظریه نسبیّت عام شکل بدهد.

اما بر خلاف نظریه نسبیت عام، که از مزیّت استقرار بر یک قلمروی نسبتاً مستقل از ریاضیات محض برخوردار است، نظریه نوظهور کوانتوم طی همین برهه می‌کوشید تا برخی مشاهدات ناملموس را با تمهیداتی که رفته‌رفته از قلمروی ریاضیات کلاسیک و سپس ریاضیات ماتریسی و موجی به عاریت می‌گرفت، توجیه بکند. این مشاهدات، از آزمایش دو-شکاف توماس یانگ در اوایل قرن نوزدهم آغاز می‌شد و تا کشف پدیده رادیواکتیویته، کشف الکترون، شکل کلّی نمودار تابش جسم سیاه، پدیده فوتوالکتریک، آزمایش قطره روغن میلیکان، آزمایش ورقه طلای رادرفورد، آزمایش اشترن-گرلاخ و ... ادامه می‌یافت. و در تمام طول این مدت نیز پیرنگی از آنچه که در اواسط دهه ۱۹۲۰ به پیدایش «نظریه نوین کوانتوم» انجامید در حال شکل گرفتن بود.

نتیجه این شد که نظریه نوین کوانتوم، اگرچه از حیث ریاضی به نظریه‌ای کاملاً موثق (و در واقع از موثق‌ترین نظریات تاریخ علم) بدل شد، اما هرچه گذشت، چیزی از شگفتی توصیفات آن از جهان بیرون کاسته نشد. مشاهدات شگفت‌انگیز، صرفاً جای خود را به استدلالات شگفت‌انگیز داده بودند.

بخشی از دلیل این موضوع به پیش‌فرض‌هایی برمی‌گردد که از ابتدای تولد شاخه فیزیک اتمی، در خصوص ماهیت «ذرات» و همین‌طور طرز تعاملات فی‌مابین‌شان وجود داشت. در واقع اصطلاح «ذره» (اعم از مولکول، اتم، و ذرات زیراتمی)، به یک موجودیت خودبسنده و مستقل از سایر هم‌نوعان خود دلالت دارد؛ موجودیتی که علی‌القاعده باید بتوان آن را به‌تنهایی هم مورد بررسی‌های دقیق قرار داد. اما نظریه نوین کوانتوم، در پرتو تمهیدات ریاضیاتی خود این امکان را رد می‌کند. در واقع رفته‌رفته مشخص شد که در سلسله‌مراتب مقیاس‌ها، از جایی به بعد، باید کلیدواژه‌های فیزیک اتمی (نظیر «اتم»، «مدار»، «موقعیت مکانی»، «علّت موضعی»، «تمایز جرم/انرژی» و ...) را وانهاد و به همان توصیفات کاملاً انتزاعی نظریه کوانتوم از طرز رفتار جهان بسنده کرد. اما سؤالی که هنوز بی‌پاسخ مانده این است که دقیقاً از «کجا» به بعد؟

ورود به قلمرو بزرگ‌مقیاس

فیزیکدانان از ابتدای تدوین نظریه نوین کوانتوم، کنجکاو همین سؤال بوده و هستند. اما مبنای ریاضی این نظریه (و توسّعاً شاخه فیزیک اتمی)، به ما فقط اجازه گام برداشتن در مسیری یک‌طرفه را در تلاش برای حل این معما خواهد داد؛ مسیری با شروع از مقیاس‌های کوچک به سمت مقیاس‌های بزرگ‌‌تر، نه بالعکس.

مثلاً به پدیده‌ای موسوم به «درهم‌تنیدگی کوانتومی» (quantum entanglement) توجّه کنید: اگرچنانچه در جریان یک فرآیند فیزیکی، یک جفت‌ ذره تولید بشوند، برخی خصوصیات این دو ذره، مثلاً قطبش یا بار الکتریکی‌شان، ضرورتاً مخالف دیگری خواهد بود (مثلاً چنانچه بار الکتریکی یکی از این ذرات مثبت باشد، بار آن‌یکی ضرورتاً منفی است). اما مادام‌که محاسبه‌ای بر روی هیچ‌کدام از این ذرات صورت نپذیرفته، تعیین اینکه کدام‌شان از چه خصوصیتی برخوردار است، ممکن نیست. ضمناً برای پی بردن به این دسته از خصوصیات این دو ذره، کافی‌ست که فقط یکی از آن دو ذره را تحت محاسبه درآوریم، چراکه خصوصیات ذره دیگر قاعدتاً مخالف آن چیزی که به دست آورده‌ایم خواهد بود.

اگرچه در نگاه اول اینطور به نظر می‌رسد که خصوصیات مدنظر، تا پیش از انجام محاسبه عملاً در ذرات وجود دارند و صرفاً این ماییم که از آنها نامطلع‌ایم، اما طبق سرراست‌ترین تعبیر از ریاضیات نظریه نوین کوانتوم، این «محاسبه» است که تعیین می‌کند آن ذرات چه خصوصیتی داشته باشند. این بدین‌معناست که چنانچه مثلاً بار الکتریکی ذره A منفی به دست بیاید، معنی آن این نخواهد بود که ما در آنِ واحد مثبت بودن بار ذره B را «دانسته‌ایم»، بلکه بدین‌معناست که در آنِ واحد، ذره B بار مثبت را «کسب کرده است».

نزدیک‌ترین تعبیری هم که در چارچوب فیزیک موجود می‌توان برای یک "آنِ واحد" یافت، سرعت نور است؛ به‌طوریکه هیچ تأثیری قادر نیست که یک مسافت معیّن را با سرعتی بیش از سرعت نور بپیماید. اما در خصوص جفت‌ذرات نامبرده، آزمایشات فزاینده‌ای از اواخر دهه ۱۹۷۰ تاکنون حکایت از آن داشته که صرفنظر از میزان مسافت مابین جفت ذرات، تأثیر محاسبه در "آن واحد" بر ذره دیگر رقم خواهد خورد؛ یعنی حتی سریع‌تر از سرعت نور. از همین‌رو هم اینچنین ذراتی را به اصطلاح ذرات «درهم‌تنیده» (entangled) می‌نامند (جهت مطالعه زمینه تاریخی و ریز استدلالات منتهی به اثبات پدیده درهم‌تنیدگی کوانتومی، رجوع کنید به بخش «معمای EPR و معضل محاسبه»، از مقاله «از ماجرای لباس آبی/طلایی تا مباحثات بور/اینشتین»).

پدیده درهم‌تنیدگی کوانتومی تاکنون موثّق‌ترین معیار برای تعیین محدوده تأثیر قوانین نظریه نوین کوانتوم بوده، چراکه با افزایش دادن فاصله بین ذرات درهم‌تنیده (یا افزودن بر تعداد آنها) می‌توان رفته‌رفته مقیاس‌های جهان میکروسکوپیک را پشت سر گذاشت و دید که این پدیده‌ها تا کجا به شگفت‌زدگی فیزیکدانان ادامه می‌دهند. و امروزه طولانی‌ترین رکورد تأثیر بلاواسطه ذرات در جریان پدیده درهم‌تنیدگی کوانتومی، عدد سرسام‌آور ۱۴۳ کیلومتر است. یعنی قوانین کوانتومی حتی در چنین فاصله‌ای هم برقرار هستند.

لذا گرچه در این تردیدی نیست که گستره تأثیرات کوانتومی را تا حتی جهان بزرگ‌مقیاس هم می‌توان پی گرفت، اما قاعدتاً این گستره باید بسیار فراتر از تأثیر تنها دو ذره خاص بر یکدیگر باشد. این موضوع، به‌ویژه با کشف پدیده‌های گیج‌کننده‌ای همچون «ابرسیالیّت» (superfluidity) و «ابررسانایی» (superconductivity)، به ترتیب در اوایل دهه ۱۹۱۰ و اواخر دهه ۱۹۳۰، دیگر معمایی نیست که حتی به قلمرو فیزیک اتمی هم محدود بماند.

در دماهای نزدیک به صفر مطلق (معادل منفی ۲۷۳ درجه سانتیگراد)، ماده – صرفنظر از جنس و ابعاد آن – به حالت‌هایی درمی‌آید که نه فقط در قالب‌های سنتی گاز/مایع/جامد، بلکه اساساً در قالب فهم فیزیکدانان نمی‌گنجد.

به عنوان نمونه، یک سیم ابررسانا اساساً فاقد مقاومت الکتریکی است؛ اما مادام‌که دمای آن بالاتر می‌رود، ابررسانایی ِ خود را به‌یکباره از دست خواهد داد. اما چنانچه همین ماده را به جای یک سیم به شکل یک «ورقه» درآوریم، با بالاتر رفتن دمای آن، ابررسانایی‌اش نه به شکلی یکباره، بلکه به طریقی پله‌به‌پله و موضعی از دست می‌رود؛ به‌طوریکه تحت برخی شرایط، قسمت‌هایی از آن ورقه هنوز ابررسانا هستند حال‌آنکه سایر قسمت‌های آن چنین نیستند.

یا مثلاً «اثر هال» را مدنظر بگیرید: در سال ۱۸۷۹، فیزیکدان آمریکایی ادوین هال پی برد که چنانچه جریانی از الکتریسیته را از دو ضلع یک ورقه فلزی (مثلاً از بالا به پایین آن) بگذرانیم، و سپس آن ورقه را در معرض یک میدان مغناطیسی ِ عمود بر جریان الکتریسیته قرار دهیم، آنگاه این میدان مغناطیسی، الکترون‌های جاری را از مسیر اصلی‌شان در جهت عمود بر جریان و همراستا با میدان مغناطیسی منحرف خواهد کرد. در نتیجه، قدری از ولتاژ القایی کاسته می‌شود. از این تغییر ولتاژ (موسوم به «ولتاژ هال») می‌توان مثلاً برای ساخت حسگرهایی جهت تعیین شدت میدان‌های مغناطیسی بهره جست. اما در سال ۱۹۸۰، فیزیکدان آلمانی کلاوس فون‌کلیتسینگ، اثر هال را یک گام پیش‌تر برد:

چنانچه ورقه فلزی را با ورقه‌ای به ضخامت تنها یک اتم جایگزین بکنیم و دمای آن را هم تا نزدیکی صفر مطلق کاهش بدهیم، آنگاه با اِعمال میدان مغناطیسی مذکور، اتفاق منحصربفردی (موسوم به «اثر هال کوانتومی») رقم خواهد خورد: میزان ولتاژ عبوری از ورقهْ همواره مقادیری یکسان و دقیق اختیار می‌کند، و به مجرّد تغییر شدت میدان مغناطیسی، ولتاژ هال هم نه به‌طور پیوسته، بلکه به نحوی گسسته و با حفظ یک نسبت ثابت دچار تغییر خواهد شد. و این‌ها همه صرفنظر از جنس آن ورقه رقم خواهد خورد. یعنی اینطور به نظر می‌رسد که تحت چنین شرایطی، اساساً «ماده» دچار تغییرات مذکور می‌شود.

اگرچه کشف پدیده هال کوانتومی جایزه نوبل فیزیک ۱۹۸۵ را برای فون‌کلیتسینگ به ارمغان آورد، اما تا مدت‌ها دست فیزیکدانان از هرگونه توضیح متقاعدکننده‌ای برای این پدیده خالی بود. به نظر می‌رسید آن نورافکنی که ریاضیات کلاسیک در برابر گام‌های بلند فیزیک اتمی در طول قرن گذشته می‌افکنْد هم‌اینک این شاخه را تا پشت مرزهای فیزیک حالت جامد مشایعت کرده بود، و حال برای ورود به این حوزه، نیاز به یک ریاضیات کاملاً متفاوت حس می‌شد؛ ریاضیاتی که بتواند رفتار ماده را نه بر حسب «ذرات» تشکیل‌دهنده آن، بلکه بر حسب «چیدمان» کلّی آن ذرات توصیف و پیش‌بینی بکند.

در آن مقطع، بالغ بر ۲۵۰ سال از پیدایش چنین ریاضیاتی می‌گذشت، بی‌آنکه در این مدت هیچ احتیاجی به آن در ساحت فیزیک احساس بشود. حال، این احتیاج حس شده بود؛ احتیاج به یک منظر «توپولوژیک».

منظر توپولوژیک: سوغاتی از کونیگسبرگ

ماجرای تدوین شاخه توپولوژی، ما را به سیاحت شهر روسی ِ کالینینگراد خواهد برد؛ شهری که در قرن هجدهم جزو متعلقّات پروس بود و تحت عنوان کونیگسبرگ شناخته می‌شد. این شهر به واسطه مسیر رودخانه پرگل، به چهار خشکی مجزّا تقسیم شده است، که در آن دوران با هفت پل به یکدیگر متّصل شده بودند. پیاده‌روی‌‌های معمول یکشنبه‌های اهالی کونیگسبرگ در سطح شهر و عبور پیاپی‌شان از این پل‌ها، امروزه برای توجیه این سؤالِ ساده و پرتکرار آن‌ موقع‌شان کافی می‌نماید که: آیا می‌توان مسیری را مشخص کرد که در جریان آن، از طریق هر هفت پل، از هر چهار خشکی شهر عبور کرد و در عین حال هم بیش از یک بار از آن پل‌ها نگذشت؟

در آن مقطع، این موضوع توجّه کارل گوتلیب اِهلر، شهردار شهر دانزیگ در همسایگی کونیگسبرگ را جلب کرد، و او موفق شد که با میانجی دوست ریاضیدان‌اش هینریش کوون، مکاتبانی را در این‌باره با لئونارد اویلر، از برجسته‌ترین ریاضیدانان زمان که در سن‌پترزبورگ روسیه می‌زیست، آغاز کند. اهلر در سنین جوانی خود سخت تحت تأثیر فلسفه گوتفرید لایب‌نیتس، فیلسوف و ریاضیدان برجسته آلمانی (و همین‌طور خلف‌اش کریستین وولف) بود و کوشید تا به همین بهانه، توجه اویلر را به بحث «حساب مکانِ» لایب‌نیتس جلب کند. اما اویلر ابتدا از حل مسأله سر باز زد و در نامه‌ای مربوط به آوریل ۱۷۳۶ برای کوون و اهلر نوشت:

"... سرور عزیزم، می‌بینید که راه حل [این مسأله] چندان ربطی به ریاضیات ندارد، و نمی‌فهمم که چرا به جای هر شخص دیگری، از یک ریاضیدان انتظار دارید که به آن دست پیدا بکند؛ چراکه این راه حل [فقط] بر عقل صِرف مبتنی است و کشف آن به هیچ اصل ریاضیاتی‌ای بستگی ندارد. ... در ضمن، سرور عزیزم، جنابعالی این سؤال را به هندسه مکان حوالت داده‌اید؛ اما بنده نمی‌دانم که این رشته نوظهور به چه مربوط می‌شود و لایب‌نیتس و و وولف انتظار حل چه مسائلی را از طریق آن داشته‌اند".

اما اصرار کوون و اهلر مبنی بر اینکه حل مسأله هفت پل کونیگسبرگ، نهایتاً به ظهور شاخه‌ای جدید از ریاضیات خواهد انجامید، اویلر را به تأمل بیشتری در این مسأله ترغیب کرد. و سرانجام او متوجّه شد که گرچه این مسأله ذاتاً یک مسأله‌ هندسی است، اما از یک لحاظ با مسائل متعارف هندسه اقلیدسی تفاوت دارد: اینکه در آن، از «مسافت‌«ها صرفنظر می‌شود. مهم نیست که ابعاد آن چهار خشکی یا طول آن هفت پل چقدر باشد، مهم نحوه اتصال آنها به یکدیگر است. پس ابتدا بایستی صورت‌مسأله را از مؤلفه‌های مربوط به مسافت زدود؛ اقدامی که گرچه تا به آن مقطع در بین ریاضیدانان سابقه‌ای نداشت، اما نیم‌قرن پیش‌تر از آن، لایب‌نیتس به امکان‌پذیری‌اش اشاره کرده بود. از همین‌رو اویلر در مقاله‌ای مربوط به همان سال، و راجع به همین مسأله، می‌نویسد:

"... افزون بر آن شاخه‌ای از هندسه که با مسافت‌ها سر و کار دارد و همیشه هم مورد عنایت [ریاضیدانان] بوده، شاخه‌ سابقاً ناشناخته دیگری هم وجود دارد که نخست لایب‌نیتس به وجودش اشاره داشته، و از آن تحت عنوان هندسه مکان یاد کرده است. این شاخه ... نه ربطی به مسافت دارد و نه در محاسباتش از آن استفاده می‌شود. هنوز به طرز مشخّصی معلوم نیست که چه‌نوع مسأله‌هایی به این هندسه مکان ربط پیدا می‌کنند، و یا باید از چه راهکارهایی جهت حل‌شان اقدام کرد".

حدود یک قرن بعد، ترجمه یونانی اصطلاح "هندسه مکانِ" لایب‌نیتس (به آلمانی: Geometriam situs)، بر عنوان رساله سال ۱۸۴۷ ریاضیدان آلمانی، یوهان بندیکت لیستینگ نشست: توپولوژی. و شش سال بعد هم در مقاله‌ای از نشریه علمی نیچر، رسماً از این اصطلاح به‌منظور تمیز دادن "هندسه کیفی از هندسه متعارف که مناسبات کمّی بر آن حکمفرماست" استفاده شد.

اویلر از طریق این هندسه ثابت کرد که نمی‌توان طی یک راهپیمایی ِ واحد، از طریق فقط یک بار گذشتن از هر هفت پل کونیگسبرگ، از هر چهار خشکی آن عبور کرد. تحت هر شرایطی، از دست‌کم یک‌ پل باید دو دفعه گذشت. او برای اثبات استدلال خود، تمام مؤلفه‌های مسأله را به هفت رشته (به نمایندگی از هفت پل) و چهار گره (به نمایندگی از چهار خشکی) ساده کرد، و به نمودار زیر (سمت راست) رسید؛ نموداری که امروزه از آن تحت عنوان یک «گراف» یاد می‌شود:

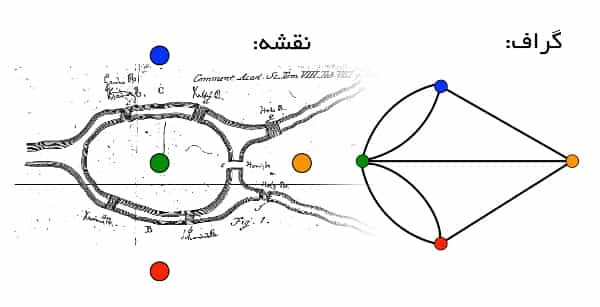
تنها مؤلفه‌ای که در این نمودار اهمیت دارد، اتصالات آن است؛ به‌طوریکه موقعیت گره‌ها و همچنین طول و شکل رشته‌ها در این بین هیچ تأثیری بر اصل مسأله نخواهد داشت. به عبارت دیگر، نمودار فوق را می‌توان به بی‌نهایت حالت دیگر هم ترسیم کرد و از منظر توپولوژیک کماکان یک شکل واحد داشت. چنانچه بخواهیم از هر چهار خشکی با عبور یک‌باره از هر هفت پل بگذریم، طبق نمودار فوق بایستی تعداد رشته‌های عبوری از هر گره (یا به عبارت امروزی، «درجه گره») عددی زوج باشد (نیمی از آنها برای ورود به خشکی و نیمی از آنها هم برای خروج از آن). این در حالی است که درجات هر چهار گره در گراف فوق، عددی فرد است. و از آنجاکه در یک مسیر پیاده‌رویْ نهایتاً دو گره در نقش نقاط شروع و پایانِ مسیر ظاهر می‌شوند، گزاره "عبور از هر چهار خشکی از طریق عبور یک‌باره از هر هفت پل"، در واقع یک گزاره‌ متناقض است. چنین چیزی ممکن نیست.

به عبارت امروزی‌تر، اویلر نشان داد که شرط ضروری امکان چنین راهپیمایی‌ای این است که گراف ما دقیقاً ۰ یا ۲ گره با درجه فرد داشته باشد؛ حال‌آنکه عملاً ۴ گره با درجه فرد دارد.

مسأله هفت پل کونیگسبرگ از این لحاظ اغواکننده است که پیچیدگی ظاهری‌‌اش ما را اشتباهاً به این تصور وامی‌دارد که «شاید» بتوان از طریق آزمون و خطا به مسیر مطلوب دست پیدا کرد. و توپولوژی، راهی برای زدودن همین پیچیدگی‌های گمراه‌کننده است؛ چراکه از منظر توپولوژیک، کلّیه مسیرهای ممکن ِ راهپیمایی‌ که از هر چهار خشکی و هر هفت پل بگذرد، مسیرهایی اصطلاحاً «همریخت» (homomorphic) هستند، و به همین‌واسطه هم هیچ‌کدام‌شان قادر به برآوردن شرط صورت‌مسأله نخواهند بود.

مثلاً حروف همریخت الفبای انگلیسی را می‌توان بر حسب تعداد «حفره»ها و «دُم»هایشان در این دسته‌ها جا داد:

۱) A، R (یک حفره، دو دم)

۲) C، G، I، J، L، M، N، S، U، V، W، Z (یک دم)

۳) D، O (یک حفره)

۴) E، F، T، Y (سه دم)

۵) H، K، X (چهار دم)

۶) P، Q (یک حفره، یک دم)

به عنوان نمونه، حروف A و R را می‌توان صرفاً با خم کردن خطوط‌شان به یکدیگر تبدیل کرد. حروف D و O را هم به همین ترتیب. اما نمی‌توان با صِرف خم کردن حرف A، آن را به شکل حرف O درآورد. چنین کاری مستلزم برش دادن و چسباندن بخش‌هایی از حرف A است. مادام‌که برای تغییر شکل دو چیز احتیاجی به برش دادن یا چسباندن اجزای‌شان نباشد، آن دو چیز از حیث توپولوژیک همریخت هستند. یعنی از منظر توپولوژیک، الفبای انگلیسی شش حرف بیشتر ندارد.

ویژگی منحصربفرد تمام توصیفات توپولوژیک این است که می‌توان هر پدیدار هندسی ِ‌ تک‌بُعدی، دوبعدی یا سه‌بعدی (اعم از خطوط، اشکال و سطوح) را بر حسب مفاهیمی نظیر همین حفره‌ها و دم‌ها تعریف کرد. و می‌دانیم که مثلاً تعداد حفره‌های یک شکل فقط می‌تواند عددی صحیح و غیراعشاری اختیار کند. مثلاً ممکن نیست که یک شکل، از ۱.۵ حفره تشکیل شده باشد.

در خصوص سطوح سه‌بعدی هم منحنی‌ها (یا به عبارت دقیق‌تر «رویه»ها) را می‌توان بر حسب بُرشی از سطح خارجی ِ یک شکل فرضی ِ n-حفره‌ای تصوّر کرد (شکلی که اصطلاحاً «رویه انتقالی» نامیده می‌شود). در واقع آن دستاوردی که مدال معتبر فیلدز را در سال ۲۰۱۴ برای مریم میرزاخانی به ارمغان آورد، ارائه رهیافتی بود که بتوان از طریق آن هر سطحی با انحنای منفی (موسوم به سطوح هذلولی) را بر حسب قطاعی از سطح خارجی یک رویه انتقالی ِ n-حفره‌ای به دست آورد؛ دستاوردی که صورت‌بندی آن برای میرزاخانی ۹ سال تمام به طول انجامید (جهت مشاهده جزئیات دقیق‌تر این دستاورد و دلالت‌های فیزیکی آن، نگاه کنید به بخش ششم از مقاله «هفت چهره منتخب علمی سال ۲۰۱۴»).

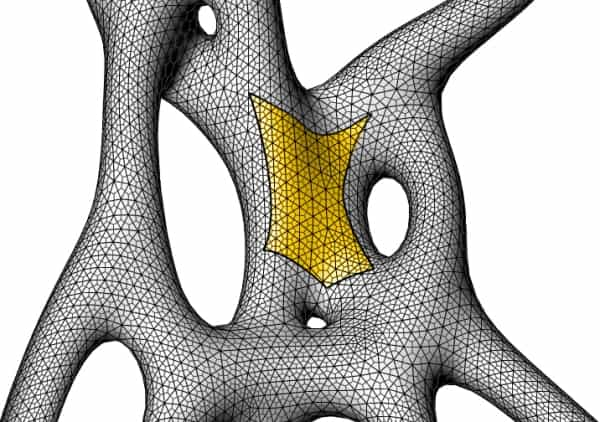
از آنجاکه برخی رفتارهای بزرگ‌مقیاس کوانتومی – اعم از ابَرسیالیت، ابررسانایی، و اثر هال کوانتومی – فقط تحت شرایط هندسی ِ خاصی (نظیر سطوح دوبعدی) پدیدار می‌شوند، و تغییراتی پله‌به‌پله (و نه پیوسته) را به نمایش می‌گذارند، به نظر می‌رسد که بتوان مؤلفه‌های پدیدآورنده‌شان را هم بر حسب توصیفات توپولوژیک درک کرد.

به عنوان نمونه، برای درک اینکه چرا هر کدام از حروف انگلیسی به یکی از دسته‌جات فوق تعلق گرفته، باید به شکل کلّی آن حرف نگریست، نه به صرفاً بخشی از آن حرف؛ به‌طوریکه این تقسیم‌بندی، فقط از یک منظر ِ کل‌گرایانهْ صائب خواهد بود. در واقع توپولوژی، زمینه را برای تعریف یک ملاک عینی برای تمیز بخشیدن مناظر «کلّی» ماده (که مبنای توصیفات شاخه فیزیک حالت جامد است) از مناظر جزئی‌نگر (که مبنای توصیفات شاخه فیزیک اتمی است) فراهم کرد. و از آنجاکه تحولات گیج‌کننده‌ای که در دماهای نزدیک به صفر مطلق در ساختار ماده دیده شده نیز تابعی از هندسه کلّی اجتماعات اتمی و نه خصوصیات تک‌تک اتم‌هاست، به نظر می‌رسد که اطلاق توصیفات توپولوژیک بر آنها رهیافت موجّهی باشد.

البته در وهله اول، اطلاق این توصیفات صرفاً راهی برای «توجیه» مشاهدات موجود بود. اما آنچه که امسال شایسته دریافت جایزه نوبل فیزیک شناخته شد، عمدتاً به «پیش‌بینی» و سپس تأیید وجود حالت‌های کاملاً تازه‌ای از ماده بر مبنای همین توجیهات برمی‌گشت: حالت‌های توپولوژیکی ماده.

توپولوژی و چشم‌اندازهای تازه‌ای فراروی رفتار ماده

تا اوایل دهه ۱۹۷۰، تصور غالب فیزیکدانان این بود که افت و خیزهای گرمایی، مانع از برقراری هرگونه نظمی در بین اتم‌های یک سطح دوبعدی می‌شوند، ولو در دماهای نزدیک به صفر مطلق. و در غیاب هیچ‌گونه نظمی هم عملاً وقوع هر «تغییر حالتی» در ماده بی‌معناست (مثلاً تغییر حالت جامد به مایع، و سپس از مایع به گاز را می‌توان فقط در گرو الگوهای متفاوت اتم‌ها ذیل این سه حالت – که هر سه نیز نظم مختص خودشان را دارند – به تصور درآورد).

با این‌همه در آن مقطع، دیوید تولس و مایکل کاسترلیتز مشترکاً تصمیم گرفتند تا این فرضیه را به بوته آزمون بسپرند؛ تصمیمی که تحت آن شرایط، توجیهی جز کنجکاوی محض دو فیزیکدان برنمی‌گرفت. و از قرار معلوم، آن‌ها بر خلاف فرض غالب فیزیکدانان، متوجه تغییراتی در حالت و الگوی سیّالیت موادی با اَشکال خاص هندسی (نظیر ورقه‌های دوبعدی، یا رشته‌های تک‌بعدی از اتم‌ها) در دماهای نزدیک به صفر مطلق شدند؛ تغییراتی که به یمن بررسی‌های پیگیر این دو فیزیکدان، فقط از منظر توپولوژیک می‌شد توصیفی قابل فهم از آنها عرضه کرد. این تغییرات که امروزه تحت عنوان «گذار کاسترلیتز-تولس» (KT Transition) شناخته می‌شوند، از جمله برجسته‌ترین کشفیات فیزیک حالت جامد در قرن بیستم به شمار می‌روند.

کمتر از یک دهه بعد، تولس تحقیقات خود را از حوزه ابرسیالیت به حوزه ابررسانایی بسط داد، و با همکاری دونکان هالدین، موفق شد تا ضرورت اطلاق مفاهیم توپولوژیکی بر این حوزه از فیزیکِ حالت جامد را نیز نشان بدهد. و به یمن همین چشم‌انداز، در سال ۱۹۸۸ او موفق شد نشان بدهد که می‌توان از طریق اثری هم‌ارز اثر هال کوانتومی، حتی در غیاب یک میدان مغناطیسی هم لایه‌های نازک نیمه‌رساناها را به ابرسیّال‌هایی توپولوژیکی بدل کرد؛ پیش‌بینی‌ای که عاقبت در سال ۲۰۱۴ به اثبات تجربی رسید.

از آن پس، پیش‌بینی‌های مشابهی راجع به سایر حالت‌های توپولوژیک ماده (اعم از سطوح سه‌بُعدی) هم مطرح شده و به تأیید تجربی رسیده است، که از برجسته‌ترین‌شان می‌توان به «عایق‌های توپولوژیک»، «فلزات توپولوژیک»، و «ابررساناهای توپولوژیک» اشاره کرد. امروزه امیدها به مصارف عَملی این مواد، خاصه در صورت‌بندی نسل نوین سامانه‌های الکترونیک و رایانه‌های کوانتومی، بسیار بالاست.

به‌طور خلاصه، جایزه نوبل امسال را می‌توان مهر تأیید دیگری در امتداد سایر دستاوردهای فیزیک جدید بر عینیت دست‌کم برخی حوزه‌های ریاضیات محض تلقی کرد. هرچند که شاید هیچ‌گاه نتوان دریافت که تا کجا می‌توان از تمهیدات ریاضیات محض برای تدوین فرضیات فیزیکی بهره جست، اما قدر مسلم‌آنکه تا وقتی امکان اثبات تجربی این فرضیات وجود دارد، نباید حتی مسأله‌ای به سادگی هفت پل کونیگسبرگ را هم چیزی نامرتبط با جهان عینی و خالی از دلالت‌هایی به زوایای ناپیدای آن تلقّی کرد.